What is Aerodynamics? Laws and branches of Aerodynamics

Last Update: February 4, 2024.

Aerodynamics is the science of forces and how they cause objects to move through the air. Aerodynamic principles describe how an airplane can fly. Aerodynamics has impacts on everything that moves through the air, from a rocket hits to a kite flying. Aerodynamics has an impact even on automobiles since they are surrounding the air.

We can measure the forces of lift, which enable an aircraft to defy gravity, and drag. Gravity and drag are the restrictions an aircraft “feels” as it flies through the air. Aerodynamics has an impact on anything that moves through the air, including birds, rockets, and airplanes.

In particular, aerodynamics aims to clarify the fundamental concepts underlying the flight of aircraft, rockets, and missiles. To establish how well-built structures like bridges and towering buildings can withstand strong winds, it is also concerned with the design of cars, fast trains, and ships.

The ancients hypothesized about the forces at play and how they interact after observing the flight of birds and projectiles. However they didn’t understand the physical characteristics of air, nor did they make an effort to systematically research those characteristics.

The majority of their concepts are based on the belief that air provides a driving or sustaining force. These ideas largely built on the then-understood concepts of hydrostatics, which is the study of fluid pressures. Even though it was realized in the 16th century. It was the projectile’s energy of motion transferred to the catapulting apparatus, this view of air as a helping medium rather than a resistant factor lingered for centuries.

1. Laws of Aerodynamics:

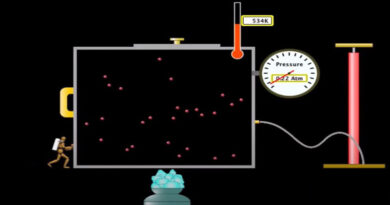
According to the premise of a fluid continuum, equations of fluid dynamics conservation are used to solve the aerodynamics issues. The three aerodynamic conservation laws are:

1.1. Conservation of Mass:

The law of conservation of mass or principle of mass conservation states that every system is shut to any move of matter and energy. The mass of the system must stay constant over time because the mass of that system cannot change, meaning that no addition to or subtraction from the system can take place. As a result, the mass remains constant over time. Although the mass may be moving in around in space or linking with entities. It may change shape, the law dictates that mass cannot be produced or destroyed.

1.2. Conservation Momentum:

The overall momentum is constant in a closed system where no matter is exchanged and no outside forces are at work. That fact is implied by the law for the conservation of momentum, one of Newton’s laws of motion. It is possible to apply the mathematical expression of this idea using Newton’s Second Law. Only external factors, including weight and viscous forces, have the power to alter a flow’s momentum. Both surface forces may be a part of this.

1.3. Conservation of Energy:

According to the principle of energy conservation, the overall energy of an isolated system stays constant over time. The energy conservation equation states that energy is never created nor destroyed within a flow and that any addition or removal of energy to a volume in the flow is caused by heat transfer or work into and out of the area of concern.

According to the law of conservation of energy, a first-class perpetual motion machine is impossible to construct, and no object is capable of supplying an endless supply of energy to its environment on its own.

These three principles work together to form the Navier-Stokes equations’ known framework. Modern aerodynamics computational methods are used to solve the Navier-Stokes equations because no analytical solution to these equations has been established.

The Navier-Stokes equations have been and are still being simplified because high-speed computer techniques were not previously available and because the computational cost of solving these complex equations is expensive now that they are. The Euler equations are a set of interconnected conservation equations that don’t take into account viscosity and can be applied in circumstances when it is thought to have a negligible effect. Another one-dimensional method for solving momentum and energy conservation equations is Bernoulli’s equation.

2. Branches of Aerodynamics:

Aerodynamics Category By the flow Environment or Flow Properties:

2.1. Compressible Aerodynamic:

According to aerodynamic theory, a flow is said to be flexible if its density changes along a streamline. This suggests that, in contrast to incompressible flow, density changes are considered.

Compressible flow typically occurs when the Mach number in all or a portion of the flow hits 0.3.

Despite being arbitrary, the Mach 0.3 value is employed because gas flows with a Mach number lower than that exhibit density variation of less than 5%.

Additionally, the item’s stagnation point experiences a 5% shift in density overall, but smaller shifts would occur elsewhere in the object.

2.2. Incompressible Aerodynamic:

An incompressible flow’s density is unchanging over time and space. Although all genuine fluids are compressible, a flow is frequently assumed to be incompressible if there is little to no effect of changes in density on the measured results.

Incompressible flow is more likely to occur when the flow rates are a little below the speed of sound.

Compressibility has a stronger effect at speeds close to or greater than the speed of sound.

If incompressibility cannot be assumed, then compressibility effects must be considered, and this is determined by the Mach number.